Stepth

Originally written 4/30/18.

In a recent math class, we were doing some introductory explorations about lines. We did an activity that Fawn Nguyen shared, called Staircase Steepness. It has students rank 6 drawn staircases by steepness, from least to most steep.

At first, students had to rank them without measuring things. They struggled with how to explain how they determined which was more or less steep. We talked about real staircases. We talked about the rise and tread of staircases. We talked about how we could “eyeball” the staircases and see which seemed more steep.

They then had to compare their rankings with peers and make decisions on which were more or less steep. Then, they got to measure. They did all sorts of different measurements. Some measured a diagonal line in different locations. Some measured the “tread” and the “rise” and then did various operations with them.

It was an interesting conversation.  One student, MV, asked if we could just do ramps (which is kind of where a “slope” lesson ends up).

As an exit ticket, I had students share something they learned or something they wondered. Some noted that there was a possibility to use the Pythagorean Theorem if you made a triangle.  A couple of them used protractors to look at angles from the base of the staircases to where the top step began. One asked, “Does it matter if the tread and rise are proportional?” One asked, “Why would we measure just one step at a time?” These are awesome questions that, when explored further, will allow for a deeper understanding of slope and rate of change, and they came about by students looking closely and noticing things they would definitely have overlooked if I had shared the “rise over run” or “change in y over change in x” explanations right away.

Another asked, “Do we use the measurements of the steps or the length and width of the whole stairs?” and “Does slope have anything to do with the activity we just did?” and “If so what are the different parts of slope and can we learn it soon?” (This student has been working ahead with her dad and still has many gaps in her understanding, but she does have a LOT of information that she often tries to share, even if I hold her back a little. I worry that jumping ahead to the procedure and the information she wants to lead us to would force us to miss out on greater conceptual understandings. I appreciate her eagerness to be there, but not everyone is where she is! Yet.) So, YES, the answer is that we ARE doing slope, but I’m not teaching procedures at this time.

…………………………………………………………………………………………………

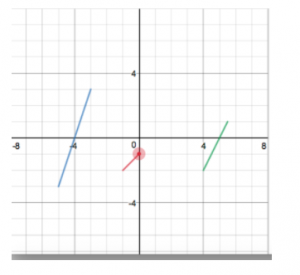
The next day, we looked at the Desmos activity, “Which is steepest?” which was the next step and connected to MV’s question about doing ramps. It looks at lines and has students select the steepest, ask for information that would be helpful, then asks them to create a line with a steepness between two other lines’ steepnesses. (At this point, a student said, “If we call deepness ‘depth’, why can’t we call steepness ‘stepth’?” So… now we refer to stepth, which will soon turn to “slope” and then be inexplicably written as ‘m‘.

Students dragged that red dot to try to make a line with a slope that’s between the steepnesses of the green and blue lines.

Here is our class overview:

What we noticed about our attempts:

• One person went in another direction, which might be a really cool way to think about this, outside the box.
• There is a darker area, where some people may have had similar ideas.
• There are some longer lines, which *might* have greater slopes.

We wondered:

• Is the line that goes downward from left to right negative, while the others are positive?
• Is there only one correct answer?
• Does it really matter how long the line is?

AB said that she tried to take the tread and the rise and multiply or divide to find what the rise would be if the tread were 1. So if we had a line with a tread of 2 and a rise of 4, she would divide both by 2, so the tread would be 1 and the rise would be 2. This brought up ideas of proportional reasoning and equivalent fractions.

We took that to the Smartboard and found our rises for the green and blue lines if their treads were both 1. We found that the blue one would be 3 and the green one would be 2. With a little trial and error, students figured that 2 ½ would work, but when they tried to move their red line, it snapped to whole numbers only. With a little practice, we were able to double the tread and move our point up to 5, so we had a 2:5 ratio, which ended up as 1:2 ½.

It was just a very interesting conversation with a lot of exciting ideas to continue to explore. (We never really touched the negative slope line, so that will come up again!)